Are there multiple levels or tiers of Conserve MP?

I was recently looking into what exactly the proc rate is for the "Augments 'Conserve MP'" property of the full Goetia attire +2 set (5/5), which was estimated indirectly last year (a thorough overview of the set bonus, including the relationship between damage multiplier and the fraction of MP conserved, is presented at The Black Mage's Apprentice in two posts). This was done by estimating the effective rate of observed procs, or the product of the actual augment proc rate (which itself cannot be observed directly when the Conserve MP rate is not 100%) and the proc rate of BLM's Conserve MP trait, which is supposed to be 25%. If you believe the set proc rate is a multiple of 5, then 15% and 20% are plausible estimates.

While some of the reasonable assumptions underlying the analysis caught my interest, such as whether the occurrences of Conserve MP, resists, magic critical hits and the Goetia set bonus are all actually mutually independent (kind of similar to whether the Double Attack trait procs on two hits of a multi-hit WS; no one actively looks for these rare events so you have to use more clever methods of providing evidence of such), of greater interest was the suggestion that there are multiple "tier"s (or "ranks" or "levels") of Conserve MP.

I just checked wiki.ffo.jp for the Conserve MP article and found a claim of at least one more Conserve MP "rank" at level 76 for BLM and level 96 for SCH. The claimed Conserve MP rate was 33%, but I couldn't find any evidence supporting this. (But there must have been some reason for this to be posted?)

I then tried to look for evidence of another tier  on the BG forums. I totally forgot I already looked at the evidence for this last year (posts #154 and #155...), and test 1 showed that the estimated Conserve MP rate for BLM was well below the claimed 33% rate. (Due to the use of a non-MVUE for the conserve MP rate, which is a binomial proportion, for the sake of convenience and sanity, the nominal 95% normal approximation confidence interval based on the binomial proportion but plugging in the non-MVUE actually has a lower coverage probability, or 91% as I claimed previously...).   This was before the September 2011 version update raised the maximum job level to 95, so this doesn't rule out any new levels being introduced since then.

So as long ago as June 2011 there did not appear to be evidence of multiple tiers of Conserve MP. If this is to be checked again in the future, the data collection procedure as described on the BG forums (see the previous link) would be one way to amass evidence for or against multiple tiers.

Aspir and Drain modeling: an incomplete picture

Earlier, I made some bold statements (at least by my standards) about the distribution of unresisted values of Drain and Aspir. I proposed a model from which I can make explicit, testable predictions.

Specifically, I wanted to see if the model holds at 114 dark magic skill, which can be attained by subbing /DRK on any job without any native dark magic skill (in my case NIN/DRK). Based on the model I described previously, the maximum Aspir without any potency-increasing equipment used is 114/3 + 20 = 58 MP, and the minimum is half that, or 29 MP.

I went out to cast Aspir on Stone Eaters (North Gustaberg (S)) and after the seventh cast I obtained an Aspir of 63 MP, which exceeds the stipulated maximum, so the model doesn't hold for 114 dark magic skill. The following are the observed data values (in order observed):

51 44 56 49 25 51 63 53 35 62 62 46 41 32 44

I then cast Drain on the same Stone Eaters with 246 dark magic skill (NIN75/SCH35 with Dark Arts) and obtained the following results (stem-and-leaf plot):

   6 | 49
   7 | 
   8 | 4
   9 | 
  10 | 
  11 | 
  12 | 
  13 | 4445
  14 | 68
  15 | 044
  16 | 46
  17 | 37
  18 | 9
  19 | 4
  20 | 23789
  21 | 79
  22 | 026
  23 | 55
  24 | 277
  25 | 36
  26 | 01346

(The reason I used Drain and not Aspir was that my scholar is only level 35, and Aspir is accessible at level 36. I would prefer to gather data for Aspir because Aspir values are obviously less variable than Drain values.)

Given 246 dark magic skill, the predicted maximum for Drain is 266 and the predicted unresisted minimum is 133 (both without any potency gear or day/weather effects), so the distribution of Drain (as represented by the sample) seems consistent with the model.

In conclusion, if one were to be technical in describing the scope of the model I proposed earlier, I would say the model is (likely) valid for Drain between 246 and 300 dark magic skill. It is valid for Aspir between 269 and 300 dark magic skill. And, finally, it is valid for Drain II between 285 and 300 dark magic skill. What happens in the 100s is just not that relevant. (In case you are wondering what data I am referring to, you'd have to check my old posts on Drain and Aspir).

Drain and Aspir minimum and maximum

Figuring out things that were already figured out years ago

After reviewing all my posts on Drain and Aspir, I finally realized that I had enough information to specify the minimum and maximum unresisted values, as a function of dark magic skill, for both Drain and Aspir, and since the distribution of unresisted values can be considered approximately uniformly distributed (acknowledging flooring effects), the mean Drain and Aspir can also be specified with reasonable certainty.

Of course, this was something that was figured out years ago. This Drain and Aspir summary page (JP) has some interesting things to say about Vampiric Mitts/Boots, Diabolos's Pole, Y's Scythe, and factors other than equipment, day/weather, and magic burst affecting Drain that do not affect Aspir, but I will leave it to those interested to check out that source while I summarize the the minima and maxima for Drain, Aspir, and Drain II, and speculate on those for Aspir II.

All specified extrema are defined for dark magic skill between 0 and 300, and for clarity's sake, factors that increase Drain or Aspir potency are not included in the statements aside from dark magic skill. It should be understood that any of those other factors increase the maximum and minimum by some multiplicative constant, and these constants can be multiplied in succession (generally, the order of multiplication is first the constant for equipment, then that for day/weather, then that for magic burst, with some twists on Drain potency you can look up yourself) with flooring after each multiplication step to obtain the final values of the maximum and minimum.

Maximum and minimum of Drain

The maximum unresisted Drain is

skill + 20,

and the minimum unresisted Drain is

floor(0.5(skill + 20)).

It follows that the mean unresisted Drain is approximately

0.75(skill + 20).

Currently 320 HP is the highest possible Drain return before any other potency-increasing factors are considered.

Each 1-point increase in dark magic skill (up to 300 total skill) increases the maximum Drain by 1 HP. Other potency-enhancing factors can increase the magnitude of this marginal return.

Maximum and minimum of Aspir

The maximum unresisted Aspir is

floor(skill/3 + 20),

and the minimum unresisted Aspir is

floor(0.5floor(skill/3 + 20)).

It follows that the mean unresisted Aspir is approximately

0.75(skill/3 + 20).

Currently 120 MP is the highest possible Aspir return before any other potency-increasing factors are considered.

Each 3-point increase in dark magic skill (up to 300 total skill) increases the maximum Aspir by 1 MP. Other potency-enhancing factors can increase the magnitude of this marginal return.

Maximum and minimum of Drain II

This discussion of the Hirudinea Earring effect (Hirudinea Earring seems to increase the potency of Drain or Aspir by either 2.5% or 3%) also has Drain II data that is consistent with the following expressions for the minimum and maximum of Drain II.

One thing to note is that Drain II has less variability than Drain I. (A dot plot would help show this.) Another thing to note is that the observed minima seem as though they are based on the expression for the maximum of Drain I. Then the minimum unresisted Drain II is

skill + 20.

The maximum unresisted Drain II is

skill + 85.

The mean unresisted Drain II is

skill + 52.5.

Each 1-point increase in dark magic skill (up to 300 total skill) increases both the minimum and maximum Drain II by 1 HP. Other potency-enhancing factors can increase the magnitude of this marginal return.

Currently 385 HP is the highest possible Drain II return before any other potency-increasing factors are considered.

Note that unlike Drain and Aspir, the variability of Drain II values appears not to vary with dark magic skill. Instead, varying skill merely shifts the distribution of unresisted values to the left or the right.

Minimum and maximum of Aspir II?

While I have yet to see anything regarding Aspir II, I wouldn't be surprised to see the minimum be

floor(skill/3 + 20)

and the maximum be

floor(skill/3 + 85),

but this is subject to verification based on others' experience.

Summary

The following table (image) summarizes the maximum, minimum and (approximate) mean unresisted value of Drain, Aspir, and Aspir II as a function of dark magic skill ("capping" at 300 skill) when no other potency-increasing factors are present.



Other potency-increasing factors increase the minimum and maximum by their corresponding multiplicative constant (e.g. that for equipment), with flooring after each multiplication step.

Increasing Drain potency

This is the last of a series of posts describing my investigation of Drain mechanics, particularly what things increase Drain potency and by how much. The following findings are based yet again on casting Drain on Zvahl Fortalices, details of which (justification, limitations, and whatnot) I described in previous posts (but weren't that detailed).

The motivation: Excelsis Ring

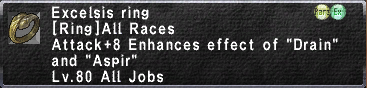
Having received the Excelsis Ring from the Bastok sequence of Wings of the Goddess nation-oriented quests, I wondered whether this ring actually increased the potency of Drain, which should be understood as increasing the maximum Drain or the average (mean) Drain value.

Having previously shown that Drain potency could possibly "cap" at 300 dark magic skill holding all other relevant factors fixed, I felt that it would be useful to verify, in the process of determining whether Excelsis Ring actually increases Drain potency, that Drain potency doesn't increase at higher levels of skill (again), specifically 331 dark magic skill.

After establishing two baseline samples at 331 dark magic skill given no other potency-enhancing equipment (or day/weather effects), I then obtained a sample adding Excelsis Ring to the "baseline." After that, I figured it would be helpful also to quantify the effects of Pluto's Staff and Dark weather on Drain potency, both relative to the baseline.

Wait a second... aren't you ever going to describe an experimental procedure in more detail?

I could, but seriously, is it that hard to think of equipment swaps that guarantee your current HP is 350-400 HP lower than your maximum HP? Hint: HP-increasing equipment upon Drain casting counts. Also, it isn't that hard to think of ways 331 dark magic skill can be attained. I could take a screenshot of the equipment used, but that would mean logging into the game.

Results

The above image is yet another set of dot plots providing a visual summary of the five samples obtained. In the past, I made no statements about the actual distribution of Drain (controlling for resist level), but by now it should be pretty obvious that a uniform distribution is a good model for the data, so further insights will be based on this model.

Also, there were a few Drain resists observed, but as they are obviously resists they can be ignored for the purposes of potency estimation, and the vertical lines denote the suspected minimum (160 HP) and maximum HP (320 HP) drained for the control samples, to be discussed later. A table (ASCII, yes I am that lazy) summarizing the extrema and median of the unresisted Drain values for each sample follows:

                    ·--------·-------------·-------------·------------·
                    |    n   |   Minimum   |   Maximum   |   Median   |
·-------------------·--------·-------------·-------------·------------·
|   Baseline 1      |   48   |       162   |       305   |    223.0   |
|   Baseline 2      |   50   |       160   |       319   |    238.0   |
|   Excelsis Ring   |   51   |       171   |       336   |    255.0   |
|   Pluto's Staff   |   61   |       184   |       365   |    263.0   |
|   Dark weather    |   30   |       190   |       349   |    288.5   |
·-------------------·--------·-------------·-------------·------------·

Speculating on what the extrema could tell us, it looks as though the variability of the data (as indicated by the range of observed values) is highest for Pluto's Staff, which is consistent with the idea that Pluto's Staff increases potency by some multiplicative factor. Also of interest is the possibility that the minimum is merely half of the maximum, so the observed minima could provide some insight on what the maxima should be.

Another obvious thing to note is that even at 331 dark magic skill, there is still no evidence that Drain potency is higher compared to that at 300 skill, so it is reasonable to conclude, considering all the data to date, that the Drain "cap" (holding other potency-enhancing factors fixed) seems to be met somewhere near 300 dark magic skill (if not exactly at 300). Technically, I could invoke an equivalence test yet again (as I did in a previous post), but you would have to be a tool to demand one here.

Since we know that a Pluto's Staff and single Dark weather each increase direct-damage magic (as shown by changes to the initial damage of any of the Bio spells, allowing for truncation) by 15% and 10% respectively, it wouldn't be surprising if these factors increased Drain potency by the same amount. It stands to reason that Excelsis Ring could behave in the same way (but increasing potency by a lesser amount).

One way to estimate the mutiplicative factors is to divide the observed maximum Drain for each of the non-baseline samples by the observed maximum for the baseline samples combined.

Excelsis Ring appears to increase Drain potency by a percentage near (336/319 - 1)100% = 5.3%. But I suspect the maximum Drain for the baseline is 320 (I just wasn't lucky enough to observe it), which would mean the increase in Drain potency from Excelsis Ring could be 5%.

Keeping in mind that the maximum Drain for the baseline could be 320, then Pluto's Staff appears to increase Drain potency by 15%, and Dark weather appears to increase Drain potency by 10%, and these figures are consistent with their effects on direct-damage magic.

An alternative, more statistical method of potency estimation is to divide the mean Drain value for each non-baseline sample by the mean Drain value of the pooled baseline sample. The ratio is then an estimate of the multiplicative factor for the potency-increasing equipment of interest. From the basic bootstrap, a set of simultaneous 95% confidence intervals for the ratios of the means can be obtained.

                    ·----------------·-------------------------------·
                    |   Mean ratio   |   Confidence interval (95%)   |
·-------------------·----------------·-------------------------------·
|   Excelsis Ring   |     1.088056   |        (0.996482, 1.183355)   |
|   Pluto's Staff   |     1.144933   |        (1.057611, 1.237342)   |
|   Dark weather    |     1.193882   |        (1.085225, 1.303625)   |
·-------------------·----------------·-------------------------------·

(Edit: 07/24/2010. I realized the bootstrapped data also included Drain resists. Not correct to include them in the data. Estimates have been corrected.) Not surprisingly, statistical significance for the potency effect of Excelsis Ring isn't achieved, but this is merely a consequence of the sample size. The effects of Pluto's Staff and Dark weather are large enough to yield statistical significance.

Conclusion and open issues

Excelsis Ring appears to increase the potency of Drain by 5%. Pluto's Staff was verified to increase the potency of Drain by 15%, and single Dark weather was verified to increase the potency of Drain by 10%.

Now, this still leaves the accuracy effect of Excelsis Ring to be determined, but quantifying it is difficult as it likely does not impart a large accuracy bonus (if there is one at all). If I were to do so, I'd be interested in determining whether Dark weather or Darksday has an effect on Drain accuracy. If so, it wouldn't be unreasonable to generalize to other types of magic and conclude that the weather or day can affect magic accuracy in general.

Regarding the mechanics of Drain in particular, it seems that the distribution of Drain could be uniform (discrete or continuous with truncation, it doesn't really matter) and that it is parameterized only by the maximum, with the minimum possibly being exactly one-half the maximum. Provided that this holds, one obvious implication is that the variability of Drain increases with dark magic skill (up to a point), and that it also increases with other various potency factors present. Taken altogether, these factors can make it very difficult to draw any conclusions about Drain (and Aspir by analogy) based on eyeballing alone.

As far as the distribution of Drain values given some sort of resist, it still isn't clear how resists relate to non-resists, but resists aren't that interesting to me so I would never willingly investigate Drain resists.

Finally, why have I never made any explicit claims about what the actual value of the Drain cap should be? Considering that Zvahl Fortalices take increased magic damage, it's possible that they also take increased Drain damage, and 320 might not be the "true" cap given that no other potency-enhancing factors are in play. But I was interested in differences, not actual amounts.

Does Drain have a cap?

This is a continuation of a line of inquiry regarding the mechanics of Drain, specifically whether an "unconditional" maximum value of Drain exists (still thinking statistically...) and, if so, whether it can be achieved with a minimum level of dark magic skill such that additional skill does nothing to increase the unconditional maximum (holding all other relevant factors fixed, obviously).

To put it another way, does additional skill do nothing to increase Drain potency?

First, I supposed that a maximum Drain value could be achieved with a minimum dark magic skill of 300 (or somewhere around 300), and that 25 additional skill would therefore not change the average potency of Drain. Data were collected in the usual manner (taking care not to cast Drain with Dark weather in effect; see previous posts for more details on "experimental procedure"). All other factors affecting potency and or accuracy were held fixed for both samples. I obtained the following results:

The maximum Drain observed given 300 dark skill was 319 and the maximum observed given 325 dark skill was 318. Also note that there were more "obvious" resists under 300 skill than under 325.

Considering the data as a whole, does 25 additional dark magic skill really have no effect on Drain potency? Noting the lack of difference in maximum Drain values should be enough for most (and it is for me), but let us also consider a way to apply statistics.

First, we can treat this data as though we were doing equivalence testing, so we need to decide what average difference would be considered a sign that there is a difference in Drain potency.

Recall that last time, I observed that, given 269 dark magic skill, I observed a maximum Drain of 288. Here, I observed a maximum Drain of 319 given 300 dark magic skill. Does one point of additional skill really increase the maximum (and minimum) Drain by 1 HP? Who knows, but suppose it were the case. Then 25 additional skill would have increased the maximum (and average) Drain by 25 HP. Let us then consider any observed difference in averages between 0 and 25 to be the result of chance, provided that there really is no difference in potency. Of course, there are some observations that are obviously resists, so let us also use the crude cutoff that any values below 150 be excluded from the analysis.

By the logic of an equivalence test ("two one-sided tests"), a 90% confidence interval for the difference in average potency between 325 skill and 300 skill is (-7.003157, 19.665328). This confidence interval is completely contained in the interval [-25, 25], so from the standpoint of statistical significance one can say that 325 skill is equivalent to 300 skill as far as average potency is concerned.

Conclusions

There appears to be no difference in Drain potency between 300 dark magic skill and 325 dark magic skill, holding all other relevant factors fixed. Additional dark magic skill still appears to affect Drain accuracy beyond 300 dark magic skill, however. Drain potency could cap at 300 dark magic skill (holding other factors fixed).

Personally, these findings devalue somewhat my dark skill equipment that is devoted solely to Drain or Aspir, of which there are three pieces. Certain pieces such as Sorcerer's gloves and Wizard's tonban still provide large boosts to accuracy (at least it is expected).

INT affecting Drain accuracy, continued

This is a followup to an earlier post showing that INT affects the accuracy of Drain.

Having found a way to suppress my base INT even further, I increased the difference between the two INT "treatments" to 60 (54 INT and 114 INT). As the resist rate for 121 INT could have been floored (presumably at 5%), maybe a 7-INT decrease would result in some increase in resist rate. The following dot plots summarize the distribution of the observed data visually:


The criterion I used last time to determine a difference between two cases, the number of Drain values set "far enough" apart from the bulk of the data (over the total number of samples in each case), doesn't quite work this time, in part because it is kind of difficult to define the "bulk" of the data for the 54-INT case. (It appears that there are more resists in general by an alternative criterion of number of Drain values below 144, though, and more for the 54-INT case than the 114-INT case.)

Instead, I probably am better off relying on the two-sample t-test to demonstrate statistical significance. The sample means for 54 INT and 114 INT are 154.28 and 191.33, respectively, and the 95% confidence interval for the difference of means is (12.213, 61.898), so the evidence, taken together (including that in the last post), provides strong support for the contention that INT affects Drain accuracy (provided that all the assumptions I stated last time hold, and why wouldn't they?), specifically that increasing INT increases its accuracy (in the form of fewer resists).

The most obvious practical implications of this finding is that the "conventional wisdom" that holds prioritizing dark skill above magic accuracy above recast reduction for Drain (and Aspir by close analogy) should incorporate INT, arguably before recast reduction. Where the benefit of reducing recast timers for Drain and Aspir is not fully realized (more often than you think) and the resist rate is suspect, the opportunity cost of recast reduction is usually additional INT, and it might not be a cost worth incurring depending on the actual trade-off.

Does INT affect Drain accuracy?

(Correction: 06/18/2010. I meant /SCH instead of /DRK toward the end. I've gone mental...)

A while ago, I asserted that INT "seems likely" to affect the accuracy of Aspir and, by implied analogy, Drain, but I had absolutely nothing on which to base this assertion. Not quite as baseless is assuming that, since then, there has been absolutely no evidence presented anywhere to support or refute that assertion.

Some problems with getting data to show whether INT affects Drain accuracy

Why do I assume that? I'm not trying to be hater and talk shit, as ignorance about this is not on the level of, say, ignorance about the party-based, hidden latent effects of curry food items.

At least where examining the effect of INT on Drain accuracy is concerned, one problem is that if you're in a situation where you have good reason to believe Drain accuracy isn't "capped," you wouldn't want your HP to be low enough to allow you obtain the actual quantity of HP taken with Drain. (Low-level beetles and worms are not acceptable targets for examining Drain accuracy with level 75 jobs, and EM+ worms are not easily accessible... yet.)

Another problem, related to the first, is that the distribution of Drain still isn't known today, and "censored" values of HP drained don't help to provide insight into that. ("Censoring" is one way to describe the fact that Drain values reported in chat logs are based on maximum HP; any HP restored beyond your maximum HP does not count in the final chat log figure, so at best you only know at least how much you drained, not its actual value or whether your Drain was resisted.)

These are some of the problems that hamper data collection.

A way to avoid these problems?

If only there were a stationary target that didn't fight back, that could allow you to suppress your HP safely, for which Drain accuracy has the possibility not to be capped at level 75, and for which you could gather Drain data without interference from other players...

Zvahl Fortalices definitely satisfy the first condition, as they do not move. They also satisfy the second condition, as two of the fortalices deeper into Castle Zvahl Baileys (S) do not have any mobs wandering nearby, including Dark and Ice Elementals. Zvahl Fortalices definitely seemed like a promising candidate for Drain testing, so I actually set out to get some data to determine if INT has some accuracy effect.

That left the third and fourth conditions. Of course, I had no idea if it would even be possible for Drain accuracy not to be capped, but that would be part of the data collection anyway, with the hope that my Drain accuracy could be decreased enough to raise the corresponding resist rate above the (assumed) 5% resist rate floor. As for people doing skill-ups, I don't really begrudge them trying to maximize their skill-up opportunities, as this method of skill-up is liable to be "nerfed" come the June 21 version update.

Goals of data collection, some assumptions, and results

My way of determining whether INT has an effect on Drain accuracy is based on a simple two-sample comparison of the occurrence of resists, one sample based on "low" INT (71 in my case), and the other based on "high" INT (121). Again, this was based on the hope that my resist rate would not be floored (at 5%) for the low-INT case. This, in turn, is based on the assumption that the resist rate is floored at 5% and rises with decreasing magic accuracy. If the data shows the resist rate being above 5% for low INT, I conclude my Drain accuracy isn't capped for low INT. (That alone would not show that INT has an effect on accuracy; I would need the second sample under high INT as well.)

But what is considered a resist? Similar to the Aspir data collection I cited previously, it would be necessary to get some sense of the distribution of unresisted Drain values, with any low Drain values set "far enough" apart from the bulk of the data considered occurrences of a resist. This is the main assumption concerning the interpretation of the data (but a reasonable one).

Now, what about the other assumptions? I merely state some of them here because I simply was not interested in testing them, and I didn't collect enough data to test these assumptions anyway.

• No differences among Zvahl Fortalices that could affect the results. This is a catch-all assumption concerning possible differences in magic evasion, INT, etc., but I don't think they exist (otherwise, fuck you, SE). If it could be shown that two Fortalices have two different base INT values (even if only a +1 INT difference), you would have to wonder about other possible confounders like level difference as well (can't assume these are level 75, etc.).
• Even if there is a bonus to Drain on Fortalices, similar to a MAB bonus for elemental magic, it should still be possible to tell the difference between a resist and a non-resist. Bio II initial damage shows there is a MAB bonus, but even if there is a similar bonus for Drain (not MAB-related, of course), it shouldn't affect one's ability to distinguish between resists and non-resists.
  
• The equipment bonuses (or penalties) aside from +50 INT for the "high INT" case have no effect on the accuracy of Drain. Now, obviously, I didn't put on equipment with dark magic skill or magic accuracy (or use a Dark Staff or Pluto's Staff), leaving only base attribute bonuses and penalties. Now, if you think MND and CHR actually have an effect on Drain accuracy, I'd like to hear the justification. If there are hidden accuracy effects on my equipment, that could be a problem, though.
  
• Dark weather and Darksday have no effect on the accuracy of Drain. This is not really an assumption, as I didn't collect any data during Darksday or under Dark weather, but I just mention it anyway as they are potential confounders.
  

Now, the results. First, dot plots of the results as an initial visual impression, under low INT (top dot plot) and under high INT (below), suggest a minimum and maximum non-resisted Drain given 269 dark magic skill:


Before jumping into a discussion of the maximum and minimum Drain values, based solely on the criterion of a resist I described earlier (low values of Drain set "far enough" apart from the bulk of the data), there are 10/65 resists under low INT and 2/63 under high INT, so this data appears to provide good evidence that increasing INT increases the accuracy of Drain, especially if you think that for the 121-INT case, the resist rate was floored at 5%. I see no reason to be pedantic and report a confidence interval or p-value.

Under both low INT and high INT, the Drain maximum (unresisted) was 288 under 269 dark magic skill. It has been said that the maximum Drain and Aspir are 300 and 100, respectively, without any potency-enhancing gear (anecdotal discussion on BG), so if it can be shown that the Drain maximum is 288 under 269 skill for other mobs, you have to wonder how Drain potency actually scales with dark magic skill.

The location of the unresisted Drain minimum is less straightforward. One possibility is that it could be at 144 HP, which would be exactly half of the unresisted Drain maximum. It would be interesting if this relationship between maximum and minimum actually holds for all levels of dark magic skill (with other potency-enhancing factors presumably serving only to affect scale). One way to check this would be with with /SCH as a subjob.

And what of the relationship between the HP value of a resist and a non-resist? I actually got 29 HP under the low-INT case, and it's difficult to describe this relationship with with small samples. But small samples are enough to reach the major conclusions.

Conclusions

Based on the criterion that low values of Drain set "far enough" apart from the bulk of the observed data should be considered resists, additional INT appears to increase the accuracy of Drain. Ideally, the data collection should be repeated in an attempt to replicate this result.

Data collection could be performed using /SCH as a subjob. +50 INT (if it could be achieved) should still be able to manifest in the form of increased accuracy (provided INT does have effect), and further exploration of the relationship between dark magic skill and unresisted Drain maximum could be done, along with that between (unresisted) Drain maximum and minimum.

How to check if a Teiwaz has superior accuracy to Terra's Staff

Obviously, I am talking about the Teiwaz with elemental affinity: magic accuracy +3, not so much that I am talking about the earth-aligned Teiwaz.

It is thought that earth affinity: magic accuracy +1 is equivalent to the accuracy bonus of Earth Staff, and earth affinity: magic accuracy +2 equivalent to the accuracy bonus of Terra's Staff. If you ever read this blog, you would know that elemental NQ staves are considered to have +20 magic accuracy for the specified element, and HQ staves, +30 magic accuracy. It is postulated that elemental affinity: magic accuracy +3 corresponds to +40 magic accuracy.

Without discussing the evidence underlying the following experiment to check whether the earth Teiwaz is superior to Terra's Staff, I will describe a superiority "trial" involving relatively few casts.

Location: Alzadaal Undersea Ruins (Nyzul Isle Staging Point)
Target monster: Level 78 Qiqirn Poulterer (ranger)
Spell to cast: Stone (I)
How many casts: 100.
What to count: number of non-resisted Stone I, number of half-resisted Stone I, number of quarter-resisted Stone I, number of eighth-resisted Stone I (should be easy to identify from the magnitude of damage)

How to identify the level 78 Qiqirn Poulterer: one way to check you have found the correct level Qiqirn is to set your accuracy score to 263 and use the "check" function to find the right Qiqirn. One way to achieve this is to equip a weapon type for which you have 230 combat skill (example: BLM with max club skill). 230 combat skill corresponds to 227 accuracy. Suppose you also have 62 DEX. For a one-handed weapon (club), this means you have +31 accuracy. Then equip +5 accuracy worth of equipment (example: Chivalrous Chain) to achieve a total accuracy score of 263. Level 77 and 76 Poulterers will check "low evasion," while the level 78 Poulterer will give no evasion message. Incidentally, this implies the level 78 Poulterer has at least 293 total evasion. You can confirm the level after killing the Poulterer by noting EXP yield (200 base EXP for level 78, 230 given 15% Sanction bonus).

Total magic accuracy for this experiment: it is known reasonably well (I will not cite evidence at this time) that having 65 INT, 290 elemental magic skill, +5 magic accuracy (from equipment), and no elemental staff corresponds to having about 55% magic accuracy rate for the Stone I spell. (The level 78 Qiqirn Poulterer has 65 INT.) If your elemental magic skill is higher or lower (say 292), make the appropriate adjustments to INT and/or magic accuracy. Here, +/-1 INT is considered +/-1% magic accuracy rate (up to a point), and +/-1 magic accuracy (from equipment) is considered +/-1% magic accuracy rate, too.

Given the above, equipping a HQ staff like Terra's brings your magic accuracy up to ~85%. A "quickie" trial I ran gave 57/71 non-resisted Stone I, strong evidence of uncapped magic accuracy rate. As postulated previously, equipping a Teiwaz with earth affinity: magic accuracy +3 could bring your magic accuracy up to ~95% (the maximum rate).

Why 100 casts of Stone I on a level 78 Qiqirn Poulterer? 100 is an arbitrary figure as I am too lazy to do a power calculation, but since we know a priori that Terra's Staff doesn't even give a capped magic accuracy rate (and it shouldn't since I said it would be ~85%), it will be very easy to show that, if the Teiwaz earth affinity: magic accuracy +3 really has +40 magic accuracy, the observed data will indicate a capped magic accuracy rate. Of course, if the accuracy bonus were higher than +40, this test wouldn't be able to show that, but the in-game constraints described by the current magic accuracy "model" and a desire for a "minimal" sample size (the further away from 50%, the smaller the standard error) led to the above experimental conditions.

Considerations: avoid Qiqirn Goldsmith links. To minimize damage from ranged attacks, it is preferable to be RDM. If not, have someone spam heal you while you hammer out 100 casts in short order. It really doesn't take that long.

Questions and desired clarifications about experimental conditions may be fielded in the comments, if anyone actually gives a shit.

Credit to pchan on BG for previous work on Qiqirn Poulterers that allows for a fairly straightforward and not-onerous experiment.

Comment potpourri

More comments on the relationship between INT and effective magic accuracy

Last week I got into this "debate" about magic accuracy (BG) regarding the results of casting Stone "a bunch of times" (massive understatement) on Qiqirn Poulterers. After inspecting lodeguy's elemental magic data back in December 2008, I speculated about a model for elemental magic to explain lodeguy's results, not expecting to find any other data to provide independent confirmation for this "model." But thanks to pchan, we now have even more data for which this model agrees (assuming I'm not being irredeemably biased in my perspective) along with some new insights that I describe rather turgidly in one of my posts there.

For example, it is known that the effects of additional magic accuracy, elemental staves, and elemental magic skill appear to be cut in half when "effective" magic accuracy or "hit rate" (the output that depends on the aforementioned inputs) is sitting below 50%. This latest data shows that the effect of INT appears also to be halved below 50% (for ΔINT ≤ 10).

Perhaps more relevant is the observation that, given this data, the effect of INT could be attenuated even further as ΔINT goes further and further beyond 10. That is, it could be (statistically) significantly less than +0.5% "hit rate" for every one-point increase in INT above ΔINT > 10. However, my naive analysis is based on statistical control and not experimental control of levels of INT, the latter of which seems preferable to minimize the influence of potentially confounding factors (as unlikely as they may seem).

Curry buns

Unless RMT are dumping inventory, I don't see why anyone would still craft Coeurl Subs instead of Yellow Curry Buns. From a crafter's standpoint, crafting Yellow Curry Buns will give a slightly better yield on the average because it's only a level 54 recipe ("tier 3" achieved at 105 cooking skill) and the most typical HQ result is 8 buns instead of 6.

But the real nail in the coffin, assuming that it's true, is that the buns retain the hidden bonus of the corresponding curries. Apparently, (hope I'm interpreting this Google translation correctly), the attack cap on Yellow Curry rises to 85 when eaten in the presence of four or more people in the same party as the consumer, among other attribute differences. Amazing that it's 2009 and players still don't know this. (Well, I never used yellow curry so I didn't know.) For Red Curry, the condition is apparently the same, but the attack bonus rises from 23% to 25% (still capped at 150). If the buns retain these hidden bonuses, why wouldn't there be higher demand for Yellow Curry Buns?

Note: the bonus from eating yellow curry (buns) while in a party does not wear off upon leaving the party. Using one while not in a party yields only 75 attack, and it probably does not increase upon joining a party of sufficient size.

Milestones

Somehow I managed to update sporadically this testament to a lack of priorities for almost one year. To be honest, I wrote foremost for myself so I didn't really bother to spend much time making these entries easily digestible for a wider audience. In particular, I found an excuse to apply some basic probability and statistics to FFXI, the playing of which is also a testament to a lack of priorities and extremely poor taste. On the other hand, I did try to focus my attention on the mechanics of the game so that these entries would have some informative value--at least some people thought so--instead of being just some masturbatory self-chronicle.

I would really like to maintain this conceit, anyway, but there is not much of an empirical mentality among the so-called playerbase to provide persuasive support for any theories that are developed or serendipitously discover non-trivial things about how the game works. Maybe some dead-enders take great pride in running their mouths without putting their bullshit to the test, but I find legitimizing claims with real data and observations to be far more interesting. I thought about turning this blog into a "digest" of sorts to summarize both new and old findings and give credit to the individuals that shed some light on some aspect of game mechanics, but actually it is just too tiresome to comb forums with crap search functions and garbage "intellects" for shiny nuggets of insight. So I will just continue talking about things that interest me enough to commit to blog, even though the posting frequency based on that criterion will be very low.

Anyway, this wasn't supposed to be just some navel-gazing exercise. Instead of making individual posts for the following topics, none of which really warrants standalone status, I decided to throw them all into a single entry.

Thoughts on Aspir

I managed to finish collecting some data to check the effect of Pluto's Staff and magic accuracy +12 on the potency of Aspir and updated the dot plot:

I think it's safe to say that INT or magic accuracy (MAB too, based on tarblm's results) have no role in the potency of Aspir (and by analogy, Drain). Note that I am not bothering with statistics and just arguing informally that none of MAB, macc, and INT increased the maximum in these samples.

As far as accuracy is concerned, that is much more inconvenient to check. The main purpose of my collecting data was to visualize the distribution of Aspir values. It seems here that the range of possible values of unresisted Aspir is fairly wide. The low values of Aspir observed may also be the result of a half-resist, which may cut the unresisted Aspir value in half. Unfortunately, you can see how partially resisted Aspirs are easily confounded with unresisted Aspirs if these ideas are true. Going back to tarblm's data though, the observed Aspirs generally have much greater variability, which could be attributed to partial resists.

Chocobo racing

Haven't talked about this in a while. A few months ago I actually canceled my content ID, but I let myself get pulled back into this pit of mediocrity that is FFXI. Since then I made some effort to maintain more detailed information on my Chocobo Circuit results, particularly whether my chocobo was competing against other PCs.

Not surprisingly, few of my C1 races were uncontested. In fact, 16 of the first 20 after I returned had at least one PC chocobo and 7 of those 16 had 2 PCs. I won only nine of those races, with a pretty abysmal 3-3-1-1 record against only one other PC.

During this time I came across a testimonial of another chocobo racer, also with a SS/B/B/B chocobo, who claimed to have won 67% of his races (128-41-22). This kind of pissed me off because farming chocobucks is extremely boring and here this guy was getting nearly 2 million more gil with the same chocobo profile and similar number of races. I thought perhaps he faced much less competition on his server and that his use of leather saddles may also have been a factor in his great success. But rather than shell out another $25 bucks to SE just for a server transfer, I tried the Sheep Leather Saddle for another month to see if taking the receptivity hit would be worth it in races with one or more other PCs.

My results were even worse with the leather saddle. In 20 races, I went 8-10-0-2 with 11 contested races, and in four of those contested races, an NPC chocobo won (I placed 2nd in all four) and in one case, two NPCs actually placed 1-2. (I finished out of the top 3 in this one.) Even worse, I won only four of the uncontested races, races in which I really "needed" to win to blunt the annoyance of losing chocobucks.

I then went back to the elm saddle and am now nurturing a nine-race winning streak (four contested), by far the longest streak I ever had. During this streak, I also reached the 10-million gil mark in net earnings. I am now going out of my way to race only in "off-hours" time slots to try to get my win rate back to 50%. My current record is 107-78-24-15.

Having reached 10 million in net earnings, I calculated an approximate rate of gil per hour earned in chocobo racing based on the time (one free race per 5 minutes) and gil spent to accumulate enough chocobucks (5,846) to enter the races and the gross earnings. Including this nine-race winning streak, chocobo racing has yielded an average of 74,644 gil per hour. (I admit this figure does not include time spent running to Chocobo Circuit.) Not as efficient as the guy winning 67% of his races, but still a nice reminder that even though chocobuck farming is a real pain in the ass, at least this huge barrier to entry allows chocobo racing to provide a steady income to those who actually put up with it... assuming the C1 races aren't so congested.

Thoughts on the possibility of chain 6 solo on Ebony Puddings without Novio and Manafont

I was extremely disappointed to find out that I had died 957 times between Adventurer "Appreciation" 2008 and A.A. 2009, the majority on black mage. (If I am really appreciated, can I get a Chocobo Wand in fewer than two weeks without being lucky?) I had considered myself more risk-averse over the past year (I did not even do Dynamis at all), but in retrospect this was not true, since you tend to die a lot in pickups, soloing, and poor event linkshells.

The pain of losing experience points on black mage (never mind the bullshit conceit that losing experience points on top of losing the time and resources you wasted is a reasonable penalty) can be blunted somewhat with efficient rate of gain of EXP. But what is considered efficient? From experience, the best I can do is around 8,000 EXP/hour (estimated by the time required to burn off an Emperor Band), and that's when being somewhat vigilant about achieving chain 5 (which is trivial if you are paying attention). Anyone who claims rates of 10,000 EXP/hr solo is full of shit until proven otherwise.

Is it possible to achieve chain 6 solo without Novio, though? By the time chain 5 rolls around I almost always have insufficient MP without Aspir to mount a chain 6 attempt, an indication that my maximum MP is not high enough. Moreover, even three "tier 4" nukes tend to leave a sliver of HP (on off-weather days), meaning that I have to rely on Drain to finish off a pudding. Casting Drain on chain 4 and 5 wastes MP that could be used for chain 6. These factors, along with half-resists and weather effects, conspire to make it really difficult to achieve chain 6. If it is easier than I am pondering, I'd like to know though, but not from shit Morrigan's users who still cast AM II on puddings.

Benevolent Despot

With the advent of Fields of Valor, the prospect of not spawning Despot in a timely fashion is less unpalatable since a training regime awards 1,550 EXP in about an hour of killing 11 placeholders. And maybe those tabs will actually be useful someday. Also, soloing without desirable rewards has grown pretty tiresome. I still have a Fenrir solo (ninja) on the back burner now that Lunar Roar supposedly does not dispel reraise, but I haven't been motivated to do that yet. At the moment, Despot is the only remotely appealing "get out there and kill shit" profit opportunity with a relatively high barrier to entry (actually being able to solo it under 30 minutes to lower the chance of vultures finding you and trying vainly to MPK you).

Though not quite as enjoyable as killing Despot and hardly a consolation prize, watching hapless groups kill Despot can provide some humor to brighten the day. Not a few weeks ago, I had the "pleasure" of witnessing this quartet of PLD/NIN, NIN/DRK, BLM and MNK struggle with Despot for over 40 minutes! Apparently, it didn't occur to these people to shed enmity via teleport in order to expedite the kill. Unfortunately, even inept players win eventually, a testimony to the dominance of the lowest common denominator in FFXI. Throw infinite time and resources at something and you can triumph! (Except for Absolute Virtue.)

Spending time farming gems of the west also has given me an opportunity to "get back" at the MPKing Tarutaru Duo That Shall Not Be Named by dispatching Despot in 22-27 minutes while those oblivious assholes continue to kill placeholders long after I'm gone.

Aspir data and observations

Edit (June 5): some attempts at clarification.

What affects the accuracy of dark magic? Skill only? How about potency? How can we describe the distribution of MP absorbed with Aspir? What data are out there to support the prevailing assertions? Finding old Aspir data sets (from 2006) was easy enough, and I also collected some Aspir data on my own.

This may seem like treading old ground if not for the B.S. I cited earlier in the week. At least there is some data you can cite when making an argument now.

Regarding the 2006 data set, the writer (whom I will call "tarblm" for now) collected Aspir data from King Buffalo (lv 79-82) over six trials. Each trial involved only a single buffalo. The data were collected under one of three configurations, all with a Pluto's Staff:

• "Dark magic skill": +40 dark magic skill (above 269) was the primary factor
• "MAB": +30 MAB from equipment (relative to control) was the primary factor
• Control: 269 dark magic skill
  

The writer also noted the experience gain for each buffalo. The data are presented in a dotplot:


First, the data give the impression that some amount of dark magic skill increases the average MP absorbed, whereas MAB doesn't, confirming previous beliefs. Certainly the maximum Aspirs are higher. Low values of MP drained seem fairly rare and set apart from the rest of the data, so describing the data as coming from a uniform distribution doesn't quite work.

Was "effective" magic accuracy capped on "very tough" buffalo? I would say yes. Otherwise, level difference would have confounded the results. If there is no difference in accuracy across the trials, one could attribute the average to an increase in so-called potency alone.

To try to avoid that uncertainty about capped magic accuracy for my data, I focused my attention on low-level Tunnel Worms and collected 50 Aspir samples for each of the following conditions without a Pluto's Staff:

• Control: 77 INT, 269 dark magic skill
  
• INT: +43 INT above control (120 total)
• Dark magic skill: +22 dark magic skill above control (291 total)

Since the worms are so low in level, I just assumed my effective magic accuracy was capped. This is a major assumption but a reasonable one given magic skill level. (Correction: I earlier used a level correction argument to make this assumption. It has not been established that level difference affects mobs in the same way that it affects PCs.) The data are illustrated in the following dotplot:


Similar to tarblm's data, some amount of dark magic skill seems to increase the average MP absorbed, although the increase is not statistically significant. As magic accuracy was probably capped in this scenario, it is probably safe to say that dark magic skill would increase potency by a statistically significant amount if I had more dark magic skill to pile on. In terms of the distribution of Aspir, it seems to shift the range of possible values to the right.

INT doesn't seem to cause any change in potency. That is not to say INT doesn't affect accuracy in some way! Low values of MP (here, below 50) were infrequent and I assure you they didn't result from capping total MP. A decrease in accuracy may manifest in a higher frequency of low values, resulting in a lower average if not a shift in the range of possible values.

Note that last time I gave an example of a data set (on FFXIclopedia) that showed INT increased the average Aspir, and I said this was a potency-only effect based on the assumption of capped accuracy. Perhaps there are other confounding factors that were not cited.

Also, data overall give an impression that Pluto's Staff affects potency (one, the 2006 data are more variable, Aspirs achieve higher values despite King Buffalo being 62-72 levels higher than Tunnel Worm).

From all this, it seems reasonable to conclude that

• Dark magic affects potency (still not sure about magic accuracy attribute, e.g., from equipment)
  
• MAB does not affect potency
• INT does not affect potency but it seems likely to affect accuracy in some way. Do not confuse accuracy with potency. In a sense, increasing one or the other should still increase the average drained up to a point, but the way each does that is different. An analogy to melee attack and melee accuracy should make sense.
  
• Magic accuracy probably affects accuracy but not potency, but I haven't found nor collected any data to check this.

You may also have noticed that the maxima and sample means in the 2006 data set are larger than those in the 2009 set. I'm pretty sure the difference can be attributed to Pluto's Staff.

Dark magic and INT

This is just going to be a quick and dirty post but may motivate a more enlightened post later, but just to reinforce the ignorance exhibited by the "player base," here's another chuckle-inducing, basically worthless discussion about what affects the accuracy and potency of Aspir. Here's another discussion from idiots talking about "tests" on the potency of Aspir, but where's the fucking data? Here's an obvious question. Did anyone ever actually disentangle accuracy from potency in a controlled experiment? Or how about, if you are at some hypothesized potency cap, why would you expect potency to increase with anything?

I mean, really, assertions like "Accuracy of [Aspir] is most highly affected by Dark Magic Skill, and is not affected by Magic Attack Bonus, or INT" are based on something rather than pointless anecdote, right?

Actually, in the talk discussion of that FFXIclopedia article on Aspir, there seems to be something like a controlled experiment with random sampling, with a RDM75 (200 dark magic skill) casting Aspir on a single worm between level 10 and 12. Assuming that "accuracy" is capped in some sense on such a low-level target, it appears that INT does affect potency (just do a quick two-sample t). Sure, type I error, blah blah, but it's better than total bullshit.

Expected magic damage in terms of accuracy - more parlor talk

In some sense, having to hoard magic accuracy for so-called high-resist targets when nuking (or enfeebling, etc.) is an all-or-nothing proposition for various reasons I just made up that may incidentally be shared by others. One, these high-resist targets have such high magic "evasion" that it is completely untenable (from experience or whatever) to nuke with the same equipment you would use for Ebony Puddings. Two, even if the target of interest is not quite as resistant as, say, a wyrm or sky god, it can be difficult to ascertain what amount of magic accuracy is acceptable to reach some threshold (say 90% acc.) without personal experience (or the experience of others). Three, compared to mindless melee auto-attacking and WSing, nuking specifically is inefficient from the standpoint of theoretical damage dealt in the "long run" (MP being an important limiting factor), so it seems pragmatic to accept unconditionally the trade-off of lowering maximum magic damage for fewer resists when there is any doubt.

If there comes a time where it is easier to ascertain the magic evasion of any mob of interest (probably never given the FFXI "team's" fetish for making basic game mechanics as opaque as possible, and lack of information sharing among the "playerbase"), perhaps it can be useful to quantify the difference in overall magic damage between a "high-resist" setup (with the purpose of maximizing magic accuracy) and a normal setup for resistant NMs and whatnot. But realistically this is just another parlor talk.

A long time ago, I argued that levels of resistance for a single "nuke" can be modeled by a one-parameter categorical distribution, with the parameter being the probability that a nuke is not resisted at all (full damage). This probability will be called "overall magic accuracy" for the remainder.

To reiterate, the distribution can be described as

no resist: π
1/2 resist: π(1-π)
1/4 resist: π(1-π)²
1/8 resist: (1-π)³

This assertion was based on prior observations by me and others that multinomial count data for nukes, categorized by level of resist, seemed to conform to such a pattern. (I will not discuss the speculated motivation for the programmers to use this model, assuming it is true.) If this is a reliable model, it seems reasonable to think about the effect of overall magic accuracy on magic damage in terms of expected value.

Ignoring rounding, let X be the actual damage of a nuke (subject to being resisted) with unresisted damage D. The expected value of X can be expressed as

E[X] = D[π+0.5π(1-π)+0.25π(1-π)²+0.125(1-π)³]

Based on this expression, overall magic accuracy can be thought of as attenuating the unresisted damage of a single nuke in the long run, multiplying that damage by some factor less than 1 that is a function of π. Therefore, in making some assessment of overall magic damage as a function of magic accuracy, we don't have to consider the actual distribution of resists given π, just as players calculating physical damage don't consider the distribution of pDIF given a ratio of attack to defense.

Just as magic accuracy attenuates unresisted magic damage by some factor less than 1, magic attack bonus (MAB) amplifies magic damage by a factor greater than 1. This is illustrated and summarized with the following graph plotting these factors described (for magic accuracy and magic attack):



As you can see, when "long run" magic damage is considered, there is decreasing return to overall magic accuracy, π (the expected value computed earlier is a third-order polynomial with respect to π), and constant return to MAB. The endpoints also make sense, too. If you happen to have 100 MAB, your overall damage is twice as high. If you happen to have 100% overall magic accuracy (recognizing that this is impossible in FFXI for nukes), then there is no attenuating of your potential magic damage.

Using the model for levels of resistance I described, it is possible and simple to estimate the percent change in long-run magic damage between two equipment setups of interest. Suppose you have a normal setup with +70 MAB such that you know will achieve 60% overall magic accuracy on some target of interest (this means in the long run 60% of your nukes will be unresisted) and you are interested in assessing whether utilizing your "high-resist" setup is worth the tradeoff in potential damage. Suppose your high-resist setup has +63 MAB and +26 more magic accuracy than the normal one.

At this point, there should be no need for quantifying the relative performance increase, but perhaps you want to quantify it anyway.

Since the magic damage "formula" is just multiplying various factors together, it is easy to calculate a percent difference that is independent of base damage, INT, weather effect, etc. (all of which could be considered constant). One needs merely to identify the multiplicative factors associated with MAB (+63 and +70) and m. acc (60% and 86%). Through direct calculation,

(1.63)(0.924757)/[(1.70)(0.752)] - 1 = 0.179

In the "long run," the overall damage using the "high resist" setup will be almost 18% higher than that using the normal one.

Again, is this useful or practical? Not really. But it could serve as a theoretical framework for "theorycrafting" (oh how I hate MMORPG-related jargon).

One more time

I am fairly amused that the conclusions from lodeguy's magic accuracy experimentation and my data analysis have been used to support the shibboleth of "320 skill/120 INT" for direct-magic damage (just browsing FFXI forums periodically). Maybe "shibboleth" is too strong a pejorative, since at least this rule of thumb acknowledges that INT contributes to overall magic accuracy (even though this acknowledgment seemed to be supported mainly with anecdotes and collective experience rather than formal data collection).

Should we really care about attaining 120 INT?

As you may recall, lodeguy gave us data that suggest (informally) a critical point for ΔINT (caster's INT minus target's INT) that "connects" two distinct regimes of rate of change of overall magic accuracy with respect to INT. To summarize, before ΔINT +10, the rate of change is estimated to be 1% per 1 INT (actually a little less from statistical significance testing), and between ΔINT +10 and ΔINT +30, 0.5% per 1 INT. I only emphasize this range because there is no data to show what might happen beyond ΔINT +30. (Moreover, there was no data to suggest, as far as I can recall, the effect of INT below 50% overall m. acc. But, realistically speaking, no one is ever going to investigate these issues. This is the best we will ever get, probably.)

With that in mind, it might be interesting to get some sense of whether 120 INT is generally suitable in "endgame" to reach the second ΔINT range with the slower rate of change. To do this, one must compare 120 INT to the INT of various "endgame" mobs.

Regrettably, information about mob INT from English-language sources is either poorly documented (sequestered in obscure FFXI forum posts) or almost non-existent (seriously, does anyone give a fuck about anything other than Ebony Puddings?), and this annoyed me to the point that I attempted to calculate the INT (as well as magic defense bonus, or MDB, and reduction of magic damage taken, or MDT-) of various mobs that I faced over the past few months to get a sense of whether I was surpassing ΔINT +10 most of the time. As I said in the last post, magic damage is deterministic (level of resist is random), so it should be fairly straightforward to calculate mob INT in many cases. Of course, I could have made calculation errors or overlooked level variability for specific mobs. I will leave it to others to verify or refute my calculations.

There isn't much variety in what I do in FFXI, though. All I have is data for mobs in NW Apollyon and those for various ZNMs. First, NW Apollyon:

Monster	INT	MDB	MDT-
Bardha	75	0	0
Pluto	82	0	0
Mountain Buffalo	60	0	0
Apollyon Scavenger	62	0	0
Gorynich	72	0	0
Kronprinz Behemoth	74	0	0
Kaiser Behemoth	???	???	???

As you can see, most of the "normal" mobs have low INT so that ΔINT +10 is easily cleared. As for Kaiser Behemoth, I didn't gather enough information, but I am pretty sure it possesses some combination of MDB and MDT- traits. I also collected similar data on some ZNMs I fought several months ago:

Monster	INT	MDB	MDT-
Lil' Apkallu	60	0	1/4
Verdelet	115	0	0
Experimental Lamia	89	0	1/8
Mahjlaef the Paintorn	112	0	1/4
Cheese Hoarder Gigiroon	81	0	0
Vulpangue	78	0.20	0
Dea	62	0	0
Iriz Ima	70	0	0
Gotoh Zha the Redolent	92	0.28	1/8
Tinnin	85	0.20	0
Achamoth	65	0.16	0

Here, MDB is reported in terms of amount above 1.00. MDT- is reported in terms of fractional reduction of magic damage.

Other than Verdelet (an imp) and Mahjlaef the Paintorn (a soulflayer), all of the ZNMs have INT such that ΔINT is well above +10. Therefore, from the standpoint of optimizing overall magic accuracy (given what we know), it seems practical to exchange INT in excess of ΔINT +10 for elemental magic skill or magic accuracy. In particular, this could be useful for Tinnin, which seems to have higher magic resistance than the "lower-tier" ZNMs (probably a result of level difference) despite having "only" 85 INT.

Moreover, there could be some patterns to mob INT despite the limited information available. Beastmen and other "sentient" mob types (particularly soulflayers and imps) could have higher INT in general than other types. Magic users have higher INT in general than non-magic users (I will treat this as self-evident).

But concerning the main question, it appears, at least for most ZNMs that are worth nuking and mobs in NW Apollyon, that ΔINT +10 is surpassed most of the time. If you happen to get close to 120 INT incidentally, that's great, but not necessarily at the expense of possible improvements to magic skill/magic accuracy. For example, Dea has only 62 INT, but it is still prone to resisting Thunder IV (compared to Blizzard IV). Therefore, it would be appropriate to use Sorcerer's Petasos instead of Demon Helm +1 for the sake of improving accuracy.

None of these mobs even have INT above 120, so it's not like you would get much of an improvement to resist rates whoring INT (such that ΔINT +10 is satisfied) compared to whoring magic skill/accuracy (all things being equal).

So what about beastmen "kings" and HNMs? Bahamut ("The Wyrmking Descends") is reported to have 115 INT (from Studio Gobli, if you can actually find the documentation). (Bahamut is sentient, right? Check.) Also Jormungand is reported to have 120 INT (also from Studio Gobli). (Perhaps the example of Jormungand motivated the 120 INT figure?) Other than that, I have no other information.

Anyone can calculate mob INT, but...

... magic defense bonus (MDB) and reduction in magic damage taken (MDT-) can get in the way of calculating INT. These factors may play a role in determining overall magic damage for things like Sarameya and Tyger. Without knowing MDB and MDT- and considering the incessant flooring involved in these calculations, it is somewhat difficult to arrive at a unique set of MDB/MDT-/INT that allows you to calculate magic damage exactly without using formal optimization methods, and I am not interested in doing that.

However, this post offers some very useful facts to determine what exactly a mob's potential MDB or MDT- is. In particular,

• 1000 Needles is not affected by MDB.
• Quick Draw is not affected by MDT-.
• Damage calculations for both are independent of mob INT.

Unfortunately, I don't have access to blue mage or corsair, but these tools would be very useful if I had access to them. Practically speaking, it doesn't seem particularly appropriate to do this kind of testing during "serious" events (how seriously do you take Proto-Ultima?), but your mileage may vary (enough with the cliches!).

The seed

First, Tarutaru Times Online no longer indexes new blog entries. Second, I have decided to stop writing about FFXI in general, so this blog will not be updated further.

However, I would like to share one last thing that I am looking into at the moment. I am calculating the INT of various "Zeni Notorious Monsters" based on data I've collected over the past few weeks.

Frankly, calculating INT should be a trivial exercise since potential (maximum) magic damage is not a function of a random variable, but I wasted a lot of time looking into the effects of magic defense bonus. Before considering possible MDB, you should first consider reductions in magic damage taken. Most of the time any overall reduction in magic damage is the result of a reduction in magic damage taken, not magic defense bonus. I am not sure to what decimal place the game rounds the ratio of MAB/MDB, either, so I would mess with that only as a last resort. (To the hundredths place? Thousandths?)

To give an example, Apkallus in general appear to take a 25% reduction in magic damage (64/256). Lil' Apkallu, then, also takes a 25% reduction in magic damage. Knowing this, it is easy to confirm what Lil' Apkallu's INT is. Other ZNMs also appear to take a similar magic damage reduction.

As another example, Verdelet does not have any magic damage reduction, so it's even easier to calculate its INT.

However, I will not give out these values as I do not feel particularly compelled anymore to share basic things to a collectively ignorant "playerbase." Fine, not everyone understands basic statistics and probability, but anyone can gather data; it's even easier to gather data automatically with a parser.

Regrettably, the magic damage formula on FFXIclopedia is incorrect in various ways, most critically the application of rounding and the order of factors that contribute to the calculation. Refer to wiki.ffo.jp for the correct expression.

Tears of a clown

So that this post is not a complete waste of time, unlike the vast majority of hand-wringing and gloating cluttering TTTO over the past week post-banning (as opposed to the usual gloating and preening about acquired equipment and "accomplishments"), there were some more interesting results from lodeguy's experimentation that I did not address previously but are still interesting (they just didn't require any statistical techniques to analyze).

For direct-magic damage, does weakness to a certain element guarantee half-resists at worst?

Lodeguy demonstrated that there is a case where elemental weakness--specifically a Fire Elemental's weakness to water--guarantees half-resists for direct-damage magic at worst. He never observed anything worse than a half-resist casting Water magic over 1,000 times on a Fire Elemental. Remember that the usual distribution of resists is easily predicted (well, if you have some estimate of an "unresisted" rate to begin with), and that the proportion of quarter or "full" (1/8) resists when effective magic accuracy (no resist) is .30 is expected to be almost .50.

This observation probably does not apply to high-level Notorious Monsters with "known" elemental weaknesses. If it were true, there would be little incentive to maximize magic accuracy for such targets. I think players would generally accept the tradeoff of having few unresisted nukes in exchange for guaranteeing at least half-damage. But perhaps there is more to this phenomenon than what has been observed.

Again, I do not read Japanese so there may be something important in the discussion that I overlooked.

What is the maximum effective magic accuracy?

It is obviously 95% for direct-magic damage. Again, under the usual distribution of resists, the proportion of half resists when effective magic accuracy is 95% is .0475; for quarter resists, .002375. Note the rare quarter-resist event. A "full" resist with magic accuracy capped is even rarer, with hypothetical probability .000125, or basically a 1-in-10,000 event.

Now that that's taken care of, some idle thoughts on the duping-related bans.

Tears of a clown - my, my, how the ressentiment flies

It is obvious to me that the point of any carte blanche clause in a "terms of service" you may observe is so that the service provider has an easy out to rid itself of undesirables. I do not really care that SE reserves a prerogative to regulate its own product through banning of accounts.

Yet although SE certainly does not need to justify any bans or suspensions it metes out, the mere appearance of uneven application of "punishment" (regardless of the fact that punishment was unevenly applied) makes FFXI look even more of a joke than it already is.

That this exploit remained in place for over 18 months is enough of a joke. Never mind SE's execrable neglect of widespread RMT activity (considerably more pervasive than anything to do with Salvage) left unabated for years in a MMORPG whose conditions were extremely conducive to RMT activity (despite SE reserving carte blanche to terminate accounts), the "nerf" to Pandemonium Warden and Absolute Virtue in response to negative publicity, etc., etc.

And, anyone who thinks anyone at SE wasn't cognizant of the duping exploit at any time during the 18 or so months before the lead-up to patch-and-ban is an idiot. There is always some "snitch" who would report such a thing. I say snitch in the vein of someone who does the right thing mostly out of impure motives, like "seeing bitches get their comeuppance."

Face it, no one gives a fuck about the "integrity" of a consumer product/service like a MMORPG except immature 39-year-olds who deign to waste all their time fulminating about a trivial thing.

Of course, this doesn't stop idiots with no sense of proportion from riding SE's dick any chance they get. That SE should even pursue damages in court for duping in a video game to keep players "honest" is simply a farcical notion. Acting like SE is some poor besieged entity in a game rife with whining entitled players---most of whom, at the end of the day, despite crying about "intolerable" low drop rates in an endgame activity they voluntarily entered into, still waste their money on FFXI--is also a joke. SE and the "player community," you deserve one another.

At the end of the day, SE can merely point to your monthly credit card statements, cheater or not, and simply say, "monthly fee." Money is the prime mover, although SE sometimes seems not to act like it is.

Mr. Decay

This post will be a potpourri of topics.

Chocobo racing - Crystal Stakes results

As of this post I've raced my (good) chocobo (SS/B/B/B) 112 times in the Crystal Stakes (C1) and obtained the following results:

1st: 52
2nd: 40
3rd: 16
4-8: 4

Total: 112

I haven't seen much information on results with other chocobo configurations, except from this one forum post (chocobo attributes unknown):

1st: 27
2nd: 12
3rd: 10
4-8: 7

Total: 56

Now, I have no idea how often this other chocobo faced competing PC chocobos, but seeing another chocobo's results helps to provide some more perspective.

Is B receptivity a good hedge if it means placing 2nd relatively more often than a chocobo with lower discernment, "all things being equal" (which never happens, but let's just finish this filler post)? One one hand, I'd rather place 1st more often at the expense of placing 3rd or lower more often, as in the long run the return could be better. (One way to think of it is that it's better to place 1st and 3rd in two races than 2nd both times.)

On the other hand, I don't like farming chocobucks.

Sure, you can calculate expected gains and losses of chocobucks per race, but I won't do it because it won't motivate me in any way to raise another chocobo.

Magic accuracy - does weather and day have an effect?

Earlier (see previous post), I observed that the (effective) magic accuracy of Paralyze seemed not to be (statistically) significantly affected when Paralyze was cast during Firesday and Iceday. I tried to search for more data sets, but I didn't find anything meaningful.

Lodeguy himself seems to have said neither day nor weather have an effect (too lazy to find the actual quote), but, really, since his goal was to measure changes in (effective) magic accuracy, whether or not there is a day/weather effect (that he didn't control for and is not practical to control for) doesn't matter all that much considering the effect, if it exists, processes only 1/3 of the time. (I haven't verified this myself though.)

Anyway, I guess I could operate under the assumption that weather and day do affect resist rates. But are the effects of day and weather on accuracy (if they exist) the same in magnitude as the effects of day and weather on damage?

If you wanted to test this assumption and you have a scholar, you could see whether single weather and day combined drastically increase the accuracy of nukes of the same element. (You could also check for the reduction in accuracy of nukes of the opposite element.)

Laziness dictates that I should do a basic statistical power calcuation to obtain the number of Bernoulli trials needed to observe that a possible 20% increase in effective magic accuracy is statistically significant, given a Type I error of 5%:

Computed N Total

Actual        N
Power    Total

0.801      166

This conservative (but one-sided) power calculation (details omitted) indicates I need a total of 332 samples (166 for the trials without the effect of weather and day, and 166 for the trials with the effect) to observe statistical significance (using Fisher's exact test) with a probability of .8. And this probability assumes that this 20% increase (or reduction depending on your approach) is real.

But, I would have to make sure my effective magic accuracy, without the effect of weather and day, is somewhere above 50% and less than 75%. Based on lodeguy's data, one could figure this out for Earth Elementals (...) or, better, a Qiqirn ranger.

If weather has an effect on magic accuracy, why does Klimaform exist?

The English description of Klimaform states that the ability "[i]ncreases the magic accuracy for spells of the same element as the current weather." This statement does not really imply an existing accuracy bonus from weather before Klimaform, nor does it really imply no weather bonus before Klimaform.

Magic accuracy - revisiting data sets other than lodeguy's

A long time ago I looked at this data set and then just glossed over it while talking about lodeguy's results. But "intellectual honesty" compels me to attempt to explain the results of this other data set.

Actually I do not recall all the experimental details, but I "hope" the Ebony Puddings targeted were at the infamous Mount Zhayolm experience "camp." There, Ebony Puddings have a level of 79 or 80. (Incidentally, I noticed that these flans provide a experience point bonus of 5%, which I could not find corroboration for on FFXIclopedia.) Then that makes the observed data more "plausible."

First, it would be pretty obnoxious to say that the effect of magic accuracy increases with skill level without even acknowledging the imprecision of the estimates. If you are going to claim that, then you have to claim that one point of magic accuracy input gives an effective magic accuracy increase well above 1%, as shown below, using the nuke data from "Test III" and "Test IV" together (without the INT observations):

                            Analysis Of Parameter Estimates

                              Standard     Wald 95% Confidence       Chi-
Parameter    DF    Estimate       Error           Limits            Square    Pr > ChiSq

Intercept     1     -3.2974      0.6462     -4.5639     -2.0309      26.04        <.0001 skill         1      0.0143      0.0022      0.0099      0.0186      40.56        <.0001 macc          1      0.0179      0.0027      0.0126      0.0232      43.27        <.0001

Not only can you not argue that macc is "better" than skill, you also cannot really say with a straight face that 1 point of magic accuracy input increases effective magic accuracy by some value well above 1%. That is just ridiculous on its face.

One possible explanation for the data is that the level 79 and level 80 Ebony Puddings were not targeted in roughly equal proportions; in the worst-case scenario, puddings of one level were inadvertently targeted exclusively for "Test III," and puddings of the other level were used exclusively for "Test IV." Since lodeguy provided some evidence of a level difference penalty (or bonus), we should be wary of such a phenomenon when collecting data.

For this data and experimental setting, a potential consequence of severe imbalance in the relative proportions of level 79 and level 80 Ebony Puddings targeted is a "distortion" of the true sampling distributions associated with the "skill" and "macc" effects, "true" meaning that the distributions should have a mean of 0.01.

This can be demonstrated through simulation as a demonstration of the concept. This is not a "proof" of anything, just a whimsical example. Suppose that the difference in level penalty between a level 79 and level 80 Ebony Pudding is 10% magic accuracy. Then, using the worst-case scenario I described above, I can generate approximate sampling distributions (with many, many assumptions) for the slopes associated with the main effects.

The most important assumption for this simulation is that 1 point of skill equals 1% effective magic accuracy, and 1 point of magic accuracy input equals 1% magic accuracy output (regardless of whether this is true in reality, which I think it is).



For elemental magic skill, the approximate sampling distribution has a mean of 0.0154 (not 0.01) and a standard deviation of .00245, which is close to the standard error from the actual data.



For magic accuracy input, the approximate sampling distribution has a mean of about 0.0133 (not 0.01) and standard deviation of about .00334. The standard error from the actual data is not close to .00334, but the concept still shows the "plausibility" of the data. Moral of the story: failing to control for real effects may have deleterious consequences.

As for the apparent (lack of) effect of INT below 50% effective magic accuracy ("Test II"), if 30 INT really corresponds to a 15% magic accuracy bonus (assuming any bonuses are cut in half because of the hit rate penalty), observing no improvement (or worse) is virtually guaranteed not to happen. At this point, I would just keep this result in mind but take it with a grain of salt.

Here's the R code I used to generate the above graphs:

n = 10000

skill2 = rep(0,n)
macc2 = rep(0,n)
skill_se = rep(0,n)
macc_se = rep(0,n)

for (i in 1:n) {
 success = c(rbinom(100,1,.59),rbinom(100,1,.72),rbinom(100,1,.72),rbinom(100,1,.79),rbinom(100,1,.90),rbinom(100,1,.90))
 skill = c(rep(274,100),rep(274,100),rep(287,100),rep(284,100),rep(284,100),rep(295,100))
 macc  = c(rep(0,100),rep(13,100),rep(0,100),rep(0,100),rep(11,100),rep(0,100))
 trials = data.frame(cbind(success,skill,macc))
 model = glm(success ~ skill + macc, family=binomial(link="identity"),data=trials)
 skill2[i] = coef(summary(model))[2,1]
 skill_se[i] = coef(summary(model))[2,2]
 macc2[i] = coef(summary(model))[3,1]
 macc_se[i] = coef(summary(model))[3,2]
}


win.graph(width = 6, height = 4.5, pointsize = 12)
hist(skill2,freq=FALSE)

win.graph(width = 6, height = 4.5, pointsize = 12)
hist(macc2,freq=FALSE)